Primes and Sines
Prime numbers are a fascinating set of numbers. A prime is a number divisible by only one and itself. 11 is prime. 6 is not prime.
Primes are a subset of the counting numbers, 1, 2, 3, 4,... Prime numbers are never negative. The first few primes are 2,3,5,7,11.
1 is not considered a prime. 2 is sometimes not considered a prime. Math papers on primes might start 'Consider the set of primes starting at 3...'.
When a number is not prime it has a list of prime factors. This is part of the Fundamental Theorem of Arthimetic. The non-prime number is created by multiplying all the prime factors together. A prime factor may repeat. 18 has 2, 3, and 3 as prime factors (2*3*3=18).
Any even number is a multiple of 2. All primes numbers are odd, except 2. This is why 2 is sometimes left off the list of primes numbers.
To determine if a number, N, is prime, a simple sequence of steps can be followed.
1 - Find the list of all primes less than the square root of the number N.
2 - For each prime, p[i], in the list of primes, N/p[i].
2a - If there is no remainder from the division of any p[i], then N is not prime.
Given 21, the square root of 21 is 4. The list of prime numbers less than or equal to 4 is 2 and 3. 21/2 = 10, with 1 remainder. 21/3 = 7, with no remainder. 21 is not prime.
To create a list of primes, one follows a sequence called a prime number sieve.
First select a maximum number to be examined, say 1000.
2 is given as a prime (or ignored).
Create a list of 1000 numbers, mark all numbers as prime.
Starting with 3, add 3 to 3. In the list, at 6, mark 6 as not prime. Continue adding 3 to obtain the next multiple of 3 marking that entry in the list as not prime until the maximum number is reached, 1000.
Repeat for all odd numbers.
Examine each odd number in the list. Those entries still marked prime is the list of prime numbers less than 1000.
This is prime number sieve is very easy to write in computer code. There are various methods of optimizing the method. One such method is found in GMP. The GMP prime number sieve finds all the primes in the first ten million digits is much less than one second (running on a recent laptop).
The basic process is 1) create a list, assume a numbers are prime, 2) mark those numbers not prime, 3) examine the resulting list looking for prime numbers.
For equation [2] the value of y is 0 at every multiple of 2. Equation [2] can be viewed as marking all those numbers that are multiples of 2 and thus not prime.
y = sin(π/3 * x) [3]
For equation [3] the value of y is 0 at every multiple of 3. Again all those numbers that are multiples of three have y=0 and visually mark the number as not prime.
Now if equations [2] and [3] are shown together.
Any odd number not crossed by equation [2] or [3] is prime. 5, 7, and 11 are the next 3 prime numbers.
Any point where y=0 for either equation [2] or [3] represents a number that is not prime.
This is true for all primes up to 24. Why 24?
Any odd number less than 24 has at least 2 or 3 as a prime factor. 25 is the first number without 2 or 3 as prime number, 5 * 5.
The list of prime numbers after 3 and before 24 is 5, 7, 11, 13, 17, 19, and 23. Using just 2 prime numbers we find an additional 7 prime numbers.
If we add a new equation
y = sin(π/5 * x) [4]
Primes are a subset of the counting numbers, 1, 2, 3, 4,... Prime numbers are never negative. The first few primes are 2,3,5,7,11.
1 is not considered a prime. 2 is sometimes not considered a prime. Math papers on primes might start 'Consider the set of primes starting at 3...'.
When a number is not prime it has a list of prime factors. This is part of the Fundamental Theorem of Arthimetic. The non-prime number is created by multiplying all the prime factors together. A prime factor may repeat. 18 has 2, 3, and 3 as prime factors (2*3*3=18).
Any even number is a multiple of 2. All primes numbers are odd, except 2. This is why 2 is sometimes left off the list of primes numbers.
To determine if a number, N, is prime, a simple sequence of steps can be followed.
1 - Find the list of all primes less than the square root of the number N.
2 - For each prime, p[i], in the list of primes, N/p[i].
2a - If there is no remainder from the division of any p[i], then N is not prime.
Given 21, the square root of 21 is 4. The list of prime numbers less than or equal to 4 is 2 and 3. 21/2 = 10, with 1 remainder. 21/3 = 7, with no remainder. 21 is not prime.
To create a list of primes, one follows a sequence called a prime number sieve.
First select a maximum number to be examined, say 1000.
2 is given as a prime (or ignored).
Create a list of 1000 numbers, mark all numbers as prime.
Starting with 3, add 3 to 3. In the list, at 6, mark 6 as not prime. Continue adding 3 to obtain the next multiple of 3 marking that entry in the list as not prime until the maximum number is reached, 1000.
Repeat for all odd numbers.
Examine each odd number in the list. Those entries still marked prime is the list of prime numbers less than 1000.
This is prime number sieve is very easy to write in computer code. There are various methods of optimizing the method. One such method is found in GMP. The GMP prime number sieve finds all the primes in the first ten million digits is much less than one second (running on a recent laptop).
The basic process is 1) create a list, assume a numbers are prime, 2) mark those numbers not prime, 3) examine the resulting list looking for prime numbers.
Sines
A sine wave is a periodic wave. It repeats as much as desired.
y = sin(x) [1]
generates a periodic wave, starting at 0,0, with four points being (π/2, 1), (π, 0), (3π/2, -1) and (2π, 0). The sine wave cross y=0 at π intervals.
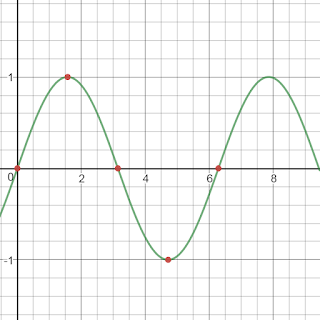 |
| y = sin(x) |
If the equation is changed to
y = sin(π/2 * x) [2]
Equation [2], starting at 0,0 has the following four points (1,1), (2,0), (3,-1), (4,0).
 |
| y = sin(π/2 * x) |
For equation [2] the value of y is 0 at every multiple of 2. Equation [2] can be viewed as marking all those numbers that are multiples of 2 and thus not prime.
y = sin(π/3 * x) [3]
 |
| y = sin(π/3 * x) |
Now if equations [2] and [3] are shown together.
 |
| y = sin(π/2 * x) and y = sin(π/3 * x) |
Any odd number not crossed by equation [2] or [3] is prime. 5, 7, and 11 are the next 3 prime numbers.
Any point where y=0 for either equation [2] or [3] represents a number that is not prime.
This is true for all primes up to 24. Why 24?
Any odd number less than 24 has at least 2 or 3 as a prime factor. 25 is the first number without 2 or 3 as prime number, 5 * 5.
The list of prime numbers after 3 and before 24 is 5, 7, 11, 13, 17, 19, and 23. Using just 2 prime numbers we find an additional 7 prime numbers.
 |
| y = sin(π/2 * x) and y = sin(π/3 * x) |
If we add a new equation
y = sin(π/5 * x) [4]
 |
| y = sin(π/2 * x), y = sin(π/3 * x), and y = sin(π/5 * x) |
It is a bit more difficult to see those numbers that are prime. 29, 31, 37, etc. are prime.
This is a graphical representation of the prime number sieve.
Take the absolute value of [2].
y = | sin(π/2 * x) | [5]
 |
| y = | sin(π/2 * x) | |
Repeat this process for equations [3] and [4].
y = | sin(π/3 * x) | [6]
y = | sin(π/4 * x) | [7]
Combine [5], [6], and [7].
 |
| y = | sin(π/2 * x) | , y = | sin(π/3 * x) | , and y = | sin(π/5 * x) | |
The numbers that are prime are now much easier to identify. The prime numbers are where the three equations lack a y=0 point.
Using [5], [6], and [7] will find the prime numbers up to 48, as 49 is 7*7. The first number without 2, 3, or 5 as a factor. The remaining primes are 7,11,13,17,19,23,29,31,37,41,43,47. With just 3 primes 12 additional primes are found.
This visualization of the prime number sieve uncovered an algorithm that seems more pleasing that the standard prime number sieve, at least to this author.
The graphs above were created using Desmos. The link to the Desmos page with the graphs is here.
Modulo code is found on GitHub.
This visualization of the prime number sieve uncovered an algorithm that seems more pleasing that the standard prime number sieve, at least to this author.
Modulo
The sine graphs are visual, but not practical. The curves are continuous. Only the values at odd numbers need to be calculated, but trigonometric functions are expensive to calculate.
It is only required to know if the sine curve is zero or not zero at the point N.
A way of determining if a number is prime is to use the same prime number list, but use modulo arithmetic instead of sines.
Modulo arithmetic was shown above for the number 21.
If a number, N, has a prime sine curve, p, passing through it (y=0) then the modulo of N of p is zero stating that N is not prime.
Given a list of primes, whose largest prime is P, for all odd numbers N from P+2 to (P+2)(P+2)-1, perform modulo arithmetic on N using the list of primes. If all modulo results are non-zero, the number is prime. Testing N can stop when one modulo result is zero.
Modulo code is found on GitHub.